For the torsion problem discussed in Section 14.6, explicitly justify the reductions in polar coordinates summarized by relations (14.6.8) and (14.6.9).

Data from section 14.6

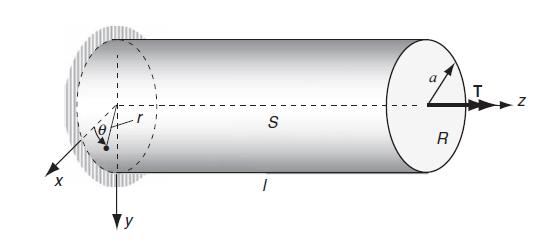
Equation 14.6.8

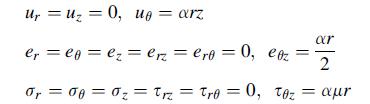
Equation 14.6.9

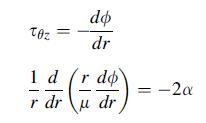
We now wish to re-examine the torsion of elastic cylinders for the case where the material is nonhomogeneous. The basic formulation and particular solutions were given in Chapter 9 for the homogeneous case and in Chapter 11 for anisotropic materials. Although a vast amount of work has been devoted to these problems, only a few studies have investigated the corresponding inhomoge- neous case. Early work on the torsion of nonhomogeneous cylinders includes Lekhnitskii (1981); later studies were done by Rooney and Ferrari (1995) and Horgan and Chan (1999c). As expected, most closed-form analytical solutions for the inhomogeneous problem are limited to cylinders of revolution, normally with circular cross-sections. Following the work of Horgan and Chan (1999c), we consider the torsion of a right circular cyl- inder of radius a, as shown in Fig. 14.24. The cylindrical body is assumed to be isotropic, but with graded shear modulus that is a function only of the radial coordinate u = u(r). The usual boundary conditions require zero tractions on the lateral boundary S and a resultant pure torque loading T'over each end section R.