Question: For Example, 11.5, consider the case of only a normal boundary load (X = 0), and assume that the material is orthotropic with i
For Example, 11.5, consider the case of only a normal boundary load (X = 0), and assume that the material is orthotropic with μi = iβi (see Exercise 11.15). Show that the resulting stress field is given by:
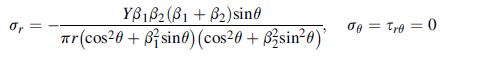
Next compare the stress component σr with the corresponding isotropic value by plotting the stress contours σr /Y = constant for each case. Use orthotropic material values for the Carbon/ Epoxy composite given in Table 11.2 and compare with the corresponding isotropic case.
Data from example 11.5

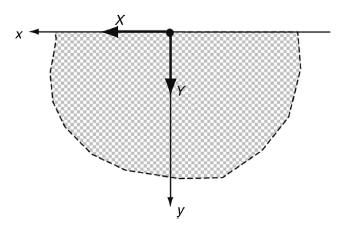
![-X = 2Re[Ai + MA1] -Y = -2Re[Ai + Ai] As before, this system is not sufficient to determine completely the](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/1/2/3/16865a21d6027b091705123166585.jpg)
Data from exercise 11.15
For the plane problem with an orthotropic material, show that the characteristic Eq. (11.5.7) reduces to the quadratic equation in μ2:
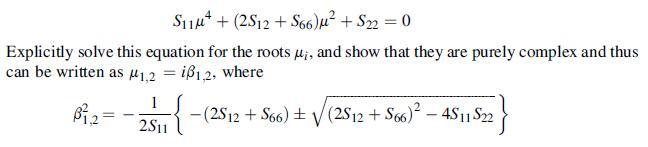
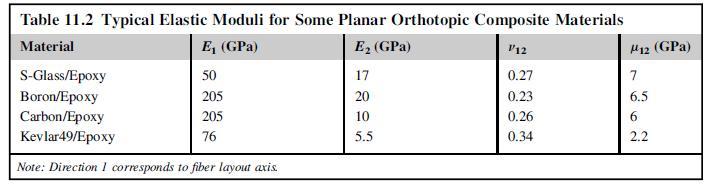
Justify the isotropic case where β1,2 = 1. Finally, determine β1,2 for each of the four composite materials given in Table 11.2. See MATLAB code C.10 for numerical methods to calculate b-parameters.
Table 11.2
or YB1B2 (B1 +82) sin Tr(cos0+ sine) (cos20+ sin0) 3 de Tre=0
Step by Step Solution
There are 3 Steps involved in it
For the case X 0 i X X BY A 2 2 B Bly iYx 1 A Z1 O 2 Resin 0 cos 0 ... View full answer

Get step-by-step solutions from verified subject matter experts


