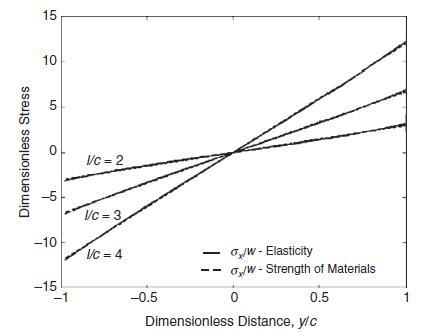
For the beam problem in Example 8.3, the boundary conditions required that the resultant normal force vanish at each end (x =± l). Show, however, that the normal stress on each end is not zero, and plot its distribution over –c

Data from example 8.3

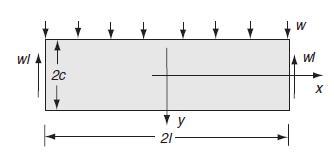
Our final example in this section is that of a beam carrying a uniformly distributed transverse loading w along its top surface, as shown in Fig. 8.3. Again, plane stress conditions are chosen, and we relax the boundary conditions on the ends and consider only statically equivalent effects. Exact pointwise boundary conditions will be specified on the top and bottom surfaces, while at the ends the resultant horizontal force and moment are set to zero and the resultant vertical force will be specified to satisfy overall equilibrium. Thus, the boundary conditions on this problem can be written as Txy(x, c) = 0 a, (x,c) = 0 oy(x, -c) = -w Last: ox(l, y)dy = 0 0,(1, y)ydy = 0 (8.1.24) try (1, y)dy = Fwl Again, it is suggested that these conditions be verified, especially the last statement. Using the polynomial solution format, we choose a trial Airy stress function including second-, third-, and fifth-order terms (a choice that has come from previous trial and error) = A20x + A21xy + A03y + A23xy 423,5 (8.1.25)