Question: For the Flamant problem with only normal loading, explore the strain energy in a semicircular area of radius R centered at the loading point. Refer

For the Flamant problem with only normal loading, explore the strain energy in a semicircular area of radius R centered at the loading point. Refer to the discussion in Section 5.8, and use relation (6.1.10) to explicitly determine the strain energy. Comment on whether the expression is singular or not as R→0.

Equation 6.1.10

Data from section 5.8

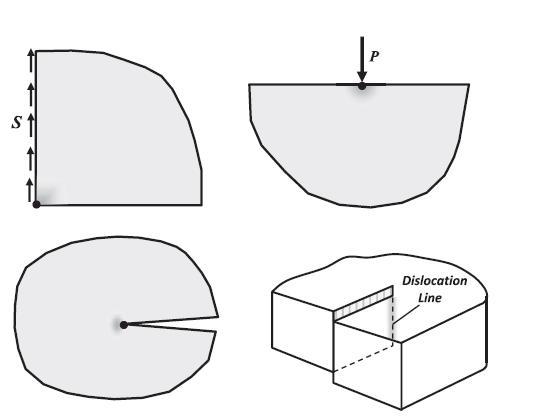
U() 1+7 2E u 2E jjkk ijij 1+v =!#(c+8+m +2c,+2+2c)-2(0,+0,+0)* 2E (6.1.10)

Step by Step Solution

★★★★★

3.31 Rating (148 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Strain Energy in terms of stress Uo 27 Flamant stress ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Elasticity Theory Applications Questions!

For the mode III crack problem in Exercise 8.44, explore the strain energy in a circular area of radius R centered at the crack tip. Refer to the discussion in Section5.8 anduse relation (6.1.10) to...

In 1911, Ernest Rutherford modeled an atom as being a point of positive charge Ze surrounded by a negative charge -Ze uniformly distributed in a sphere of radius R centered at the point. At distance...

The ends of an elastic string with a knot at K(x, y) are attached to a fixed point A(a, b) and a point P on the rim of a wheel of radius r centered at (0,0), As the wheel turns. K traces a curve C....

Summarize this for me Someone who understand MEA and HEA very well. And please make sure the summary is 2 pages . no less than 2 pages plz thanks Effects of temperature on mechanical properties and...

Welcome! Please read this page (in particular) very carefully. Instructions You need to understand how to send your assignments (deliverables) Instructor: to your instructor. The tabs (bottom of each...

Select an organisation with which you are familiar and write a report on how you would transform a clearly defined segment of the organisation into a sustainable business segment. Do not select an...

Due Sunday, 11/20: Problems from Zimmerman text: 2-11, 2-44, Case 2-3, 7-7, and 7-20 Chapter Two The Nature of Costs Chapter Outline A. Opportunity Costs 1. Characteristics of Opportunity Costs 2....

Source: Roberto Leon, Department of Civil and Environmental Engineering, Virginia Tech, Blacksburg, VAThere are two distinct stages in a construction project involving concrete. The first stage...

Managing Service Quality: An International Journal Service quality in automated teller machines: an empirical investigation Bedman Narteh Article information: Downloaded by QATAR UNIVERSITY At 22:38...

Consider the prediction problem on the MDP shown below, with transitions according to policy. The sole non-terminal state s has a self-loop with probability 1-e, yielding reward 1. With probability ,...

You used horsepower and weight to predict mileage (stored in Auto2012). Using the results from that problem, a. At the 0.05 level of significance, determine whether each independent variable makes a...

In 2015, 16.4% of Australians aged 45 to 54 years reported a disability compared to 8.2% aged 15 to 24 years (data obtained from Australian Bureau of Statistics, Disability, Ageing and Carers,...

Describe brand-based campaigns and learn the basics of display campaign management and inventory classifi cation along-with gaining knowledge on emerging data-driven display models (programmatic and...

The following equation describes the temperature T(t) of a certain object immersed in a liquid bath of constant temperature T b . Suppose the objects temperature is initially T(0) = 70F and the bath...

The following equation describes the motion of a mass connected to a spring, with viscous friction on the surface. Plot y(t) for y(0) = 10, y(0) = 5 if a. m = 3, c = 18, and k = 102 b. m = 3, c = 39...

The equation for the voltage y across the capacitor of an RC circuit is where !(t) is the applied voltage. Suppose that RC = 0.2 s and that the capacitor voltage is initially 2 V. Suppose also that...

A product has a sales price of $250 and a per-unit contribution margin of $75. What is the contribution margin ratio

During the last decade, most growth in foreign direct investment has been through joint ventures. greenfield investment. acquisitions. mergers

Lionworks, Inc. has goods available for sale in the amount of $123,000; beginning inventory is $41,000; ending inventory is $38,000; and cost of goods sold is $80,000. How many days could Lionworks...