For the torsion problem in Example 9.3, explicitly justify that the required values for the constants appearing in the stress function are given by c = 3–√8 and K=–μα/
[4a²(1–√2)]. Also calculate the resulting shear stresses and determine the location and value of the maximum stress.

Data from example 9.3

As a final example of the boundary equation scheme, consider the more general case of a section with a polynomial boundary equation. The trial stress function is taken of the form:

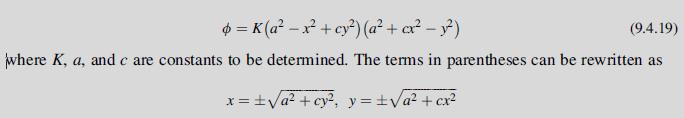
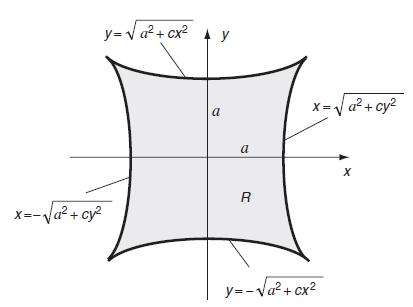
and these represent pairs of curves shown in Fig. 9.11 that can be interpreted as bounding a closed region R as shown. This region is taken as the cylinder section for the torsion problem. As before, this stress function vanishes on the boundary, and it satisfies the governing equation (9.3.9) if c = 3–√8 and K =–μα/[4a²(1–√2)]. The stresses and displacements can be calculated using the previous procedures (see Exercise 9.16). Timoshenko and Goodier (1970) discuss additional examples of this type of problem.

= K (a-x + cy) (a + cx - y) (9.4.19) where K, a, and c are constants to be determined. The terms in parentheses can be rewritten as x = a + cy, y = a + cx