Question: P(A) = 0.25, P(A') = 0.75, P(B|A) = 0.3, and P(B|A') = 0.5 Use Bayes Theorem to find P(A|B). According to Bayes Theorem, the probability
P(A) = 0.25, P(A') = 0.75, P(B|A) = 0.3, and P(B|A') = 0.5
Use Bayes’ Theorem to find P(A|B).
According to Bayes’ Theorem, the probability of event A, given that event B has occurred, is
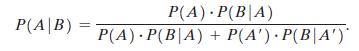
(A) : P(B|A) P() - (B|A) + P(A')- (B|A') P(A|B)
Step by Step Solution
★★★★★
3.57 Rating (161 Votes )
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock
Given that PA 025 PA 075 PBA 03 PBA 05 We are required to find PA... View full answer
Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock
Study Help