Consider the following queueing system. Customers arrive in pairs according to a

Poisson process with rate ? = 1 customer pair/minute. There is one server and room

for two customers to wait in line. Service times are exponential with mean 30 seconds.

If there is not room for both arriving customers, they both leave. (a) Describe the system

in a rate diagram and find the stationary distribution. (b) Now suppose that pairs may

split up. If there is not room for both, then with probability 1

2

they both leave and with

probability 1

2

one stays and the other leaves. Do (a) again under these assumptions.

46 Customer groups arrive to a service station according to a Poisson process with rate ?

groups/minute. With probability p, such a group consists of a single individual, and with

probability 1 ? p, it consists of a pair. There is a single server and room for two to wait

in line. Service times are exponential with rate . If a pair arrives and they cannot both

join, they both leave. (a) Give the state space and describe the system in a rate diagram.

(b) Suppose ? = and p =

1

2

. Find the stationary distribution (?0, ?1, ?2, ?3).

47 Phone calls arrive to a company according to two independent Poisson processes, one of

female callers with rate 2 and one of male callers with rate 1 (calls/minute). There is one

server and room for one to wait in line. If the server is busy, a female caller stays to wait

in line with probability 0.8; a male caller, with probability 0.5. Service times are i.i.d.

exponential with mean length 2 minutes. Let the state be the number of customers in the

system. (a) Describe the system in a rate diagram and find the stationary distribution.

(b) What proportion of callers are lost?

48 Consider an M/M/1 queue with arrival rate ? and service rate and where an arriving

customer who finds k individuals in the system joins with probability 1/(k + 1). When

does a stationary distribution exist and what is it?

49 Reneging. Consider an M/M/1 queue with arrival rate ? and service rate , where a

customer who is waiting in line reneges and leaves the line after a time that is exp(?)

(unless service has started), independent of the queue length. Describe this system in a

rate diagram and state the generator.

50 Consider an M/M/1 queue in equilibrium and let W be the waiting time of an arriving

customer. Find the cdf of W. What type of distribution is this? Hint: First find

P(W = 0), and then compute P(W > x) by conditioning on the number of customers

in the system.

51 Consider an M/M/1 queue in equilibrium and let T be the total time an arriving

customer spends in the system. Find the distribution of T (condition on the number of

customers in the system at arrival).

?

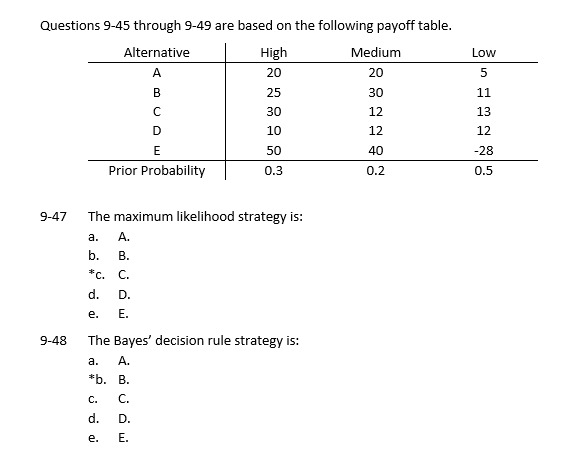
Mus 3 ) 4. For the function f(x) = x - x3 on the interval [-2, 0], state the hypotheses of the Mean Value Theorem, and M verify that f satisfies these hypotheses. Then find the number(s) c satisfying the conclusion of the Mean Value Theorem. I) Must bee- continous on Lay b] 2) Differentiable on (a, b ) 3 ) "F ( b ) -fcaz = of'(( ), for c is ( 9, b) b - a FC * ) = * - x 3 continous F' LX ) = 1 - 3 ya Differentiable F ( b ) - F ( a ) F ( 0 ) = 0-03 = 0 b - a F ( - 2 ) = - 2- 1-213 = - 2 + (+8 ) = 6 F ( b ) - F( ) = 6 - 6 -3 f( ) - fla ) b- a Now sped to jolly ficc ) = Page 2 of 4Questions 9-45 through 9-49 are based on the following payoff table. Alternative High Medium Low 20 20 5 25 30 11 30 12 13 D 10 12 12 E 50 40 -28 Prior Probability 0.3 0.2 0.5 9-47 The maximum likelihood strategy is: a. A. b. B. #c. C. d. D. e. E. 9-48 The Bayes' decision rule strategy is: a. A. *b. B. C. C. d. D. e. E.2. [1D mark{s}] You invite your friend to come to your house for dinner. They have to drive from a fair distance away, so the probability distribution of their arrival time t is uniform between 7pm and 3pm, assuming everything is going to plan. At '?:3pm, you start to worry because your friend has not arrived. Let Ill be the statement that your friend did not arrive before T:3[lpm. Let X be the statement that everything is fine1 so -IX is the statement that something is wrong. {a} [2 mark(s}] Find the probabilities P[l I X} and P[1 | :X] lets discussed in lectures, these relative frequencies or proportiors are not the same concept as the Bayesian probabilities needed for the question. but in some applications it is sensible to set them to the same values. {b} [2 marklsjl Using a Bayes Box or Bayes' rule, calculate the posterior probabilities of X and -X given DI. Use prior probabilities of 0.99 and (1.131 respectively. At T:54pm, your friend still hasn't arrived. Let D2 be the statement that your friend did not arrive before 7:54pm. {c} [3 mark(s]] Using a Bayes Box or anes' rule, calculate the posterior probabilities of X and :X given D1 and D2. Use the method where you start from the original prior probabilities and musider the data jointly. lid} [3 mark(s}] Using a Bayes Box or Bayes' rule, calculate the posterior probabilities of X and -IX given DI and D2. Use the method where your prior is the posterior from part (b) and the updating process only uses D2. Hint: You should get the same result in parts {c} and {d}. Question 9 0.5 pts Independent outcomes result in a simplified form of which rule? Conditional Probability Rule Rule of Inverse Probabilities (aka Bayes' Theorem) General Addition Rule Rule of Total Probability General Product Rule Rule of Complementary Probabilities Question 10 0.5 pts Mutually exclusive outcomes result in a simplified form of which rule? Rule of Inverse Probabilities (aka Bayes' Theorem) Rule of Total Probability O Rule of Complementary Probabilities General Addition Rule O Conditional Probability Rule O General Product Rule