Prove that the generalized logit model (5.6) can be defined with utility functions \(y_{i j}^{*}=\alpha_{j}+\boldsymbol{\beta}_{j}^{\top} \mathbf{x}+\varepsilon_{i j}\), where \(\varepsilon_{i j}\) follows the standard Gumbel distribution for each level \(j=1, \ldots, J\) and for subjects \(i=1, \ldots, n\), and that \(\left\{\varepsilon_{i, 1}, \ldots, \varepsilon_{i, \mathrm{~J}}\right\}\) are independent.

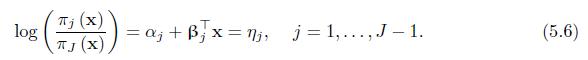
log (7 (x) (x) = a;+Bx=nj, j = 1,...,J-1. (5.6)