Dimensionless combinations of quantities (commonly called dimensionless parameters) play an important role in fluid mechanics. Make up five possible dimensionless parameters by using combinations of some of the quantities listed in Table 1.1.

Table 1.1

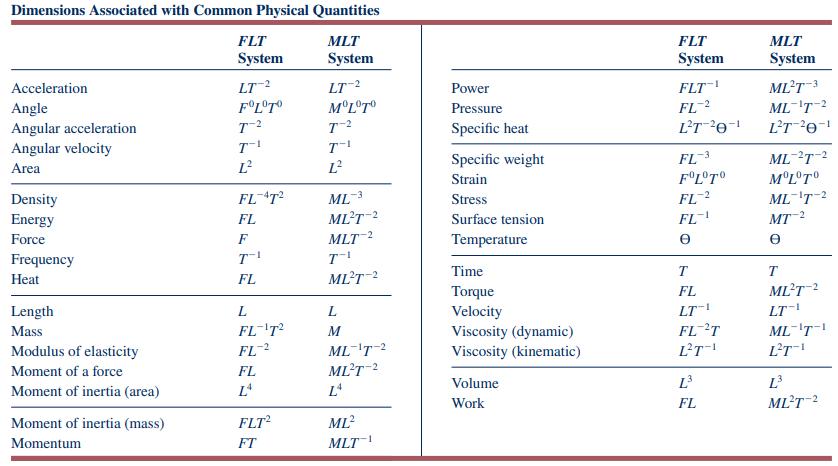
Dimensions Associated with Common Physical Quantities FLT MLT FLT MLT System System System System Acceleration LT-2 LT-2 Power FLT-1 MLT-3 Angle FLTO MLTo Pressure FL-2 Angular acceleration ML-T-2 T-2 T-2 Specific heat LT 201 LT-201 Angular velocity T-I T-1 Area L L Specific weight FL-3 ML 2T-2 Strain FLTO MLTo Density FL-4T2 ML-3 Stress FL-2 MLT-2 Energy FL MLT-2 Surface tension FL-1 Force MT-2 F MLT-2 Temperature Frequency 7-1 T-1 Heat FL MLT-2 Time T T Torque FL MLT-2 Length L L Velocity LT-1 LT-1 Mass FL-T2 M Viscosity (dynamic) FL-2T ML-'T-1 Modulus of elasticity FL-2 ML-1T-2 Viscosity (kinematic) LT-1 LT-1 Moment of a force FL MLT-2 Moment of inertia (area) L4 L4 Volume L L Work FL Moment of inertia (mass) Momentum MLT-2 FLT2 ML FT MLT 1