Water flows steadily through the variable area horizontal pipe shown in Fig. P3.3. The centerline velocity is given by \(\mathbf{V}=\) \(10(1+x) \hat{\mathbf{i}} \mathrm{ft} / \mathrm{s}\), where \(x\) is in feet. Viscous effects are neglected.

(a) Determine the pressure gradient, \(\partial p / \partial x\) (as a function of \(x\) ), needed to produce this flow.

(b) If the pressure at section (1) is \(50 \mathrm{psi}\), determine the pressure at (2) by (i) integration of the pressure gradient obtained in (a), (ii) application of the Bernoulli equation.

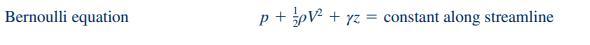
Figure P3.3

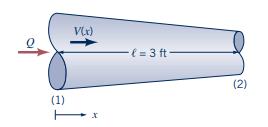
Bernoulli equation p+pv + z = constant along streamline