Question: Consider the function (u=sin x). Apply the forward difference (4.4), backward difference (4.9), and central difference (4.10) to evaluate the derivative (d u / d

Consider the function $u=\sin x$. Apply the forward difference (4.4), backward difference (4.9), and central difference (4.10) to evaluate the derivative $d u / d x$ at $x=1.0$. Use the uniform grids with steps $\Delta x=$ $1.0,0.5,0.1$, and 0.01 . Compare the results with the exact value of the derivative. Determine which grid steps give accurate results (e.g. with the error less than 0.01) for each scheme. Explain why one scheme is more accurate than the two others.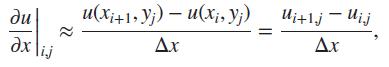 (+1, ;) - (, ) Ui+1j - Uij

(+1, ;) - (, ) Ui+1j - Uij

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Engineering Mechanics Dynamics Questions!

U.S. Steel has an invoice of $3,000,000 from a supplier. The credit terms are 2/15, net 45. U.S. Steel's cost of short-term borrowing is 5%. What is the difference in the present value of paying the...

In the same way as in Problem 1, compare the performance of the central difference scheme (4.10) and the fourth-order scheme (4.15). Problem 1 Consider the function $u=\sin x$. Apply the forward...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

interpolation and the Lagrange polynomial 5. Polynomial Irrte rpolation. {a} Use the Lagrange interpolation process to obtain a polynomial of least degree that assumes these values. 1 I] 2 3 4 y i"...

MA3310 Project Project Topic List Topic: Numerical differentiation Topics and skills: Derivatives, calculator While the rules of differentiation allow us to compute the derivative of just about any...

Module 1 Functions and Limits Project Project Topic List Topic: Numerical differentiation Topics and skills: Derivatives, calculator While the rules of differentiation allow us to compute the...

9/14/10 12:39 PM Page 381 Chapter dug84356_ch06a.qxd 6 Rational Expressions Advanced technical developments have made sports equipment faster, lighter, and more responsive to the human body. Behind...

A. B. A. B. ( ( ) ) Beginning and Intermediate Algebra An open source (CC-BY) textbook Available for free download at: http://wallace.ccfaculty.org/book/book.html by Tyler Wallace 1 ISBN...

COVER PAGE STAT 608 Homework 05 Summer 2017 Please TYPE your name and email address below, then convert to PDF and attach as the first page of your homework upload. NAME: EMAIL: HOMEWORK NUMBER:...

Larson Lumber makes annual deposits of $ 500 at 6 percent compounded annually for three years. Required: What is the future value of these deposits?

Solve the following system of ODEs using Laplace transform and matrices to solve the system 1' - y = 0 x + y' + z = 1 I - y + 2 = 2 sin t; x(0) = 1, y(0) = 1, z(0) = 1|

18. Consider the following time series data. t 1 2 3 4 5 6 7 yt 10 9 7 8 6 4 4 a. Construct a time series plot. What type of pattern exists in the data? b. Develop the linear trend equation for this...

Using team development techniques and your own experience in teams, provide suggestions for actions you can take in student teams to avoid these dysfunctions.

At time t = 0, the position vector of a particle moving in the x-y plane is r = 5i m. By time t = 0.02 s, its position vector has become 5.1i + 0.4 j m. Determine the magnitude v av of its average...

At time t = 0, a particle is at rest in the x-y plane at the coordinates (x 0 , y 0 ) = (6, 0) in. If the particle is then subjected to the acceleration components ax = 0.5 0.35t in. /sec 2 and ay =...

Given two 4-dimensional minimum bounding rectangle (MBRs) in an R-tree, A = (2, 10; 40, 60; 32, 40; -2, 11) and B = (3, 4; 30, 50; 30, 40; 20, 23), please use an MBR, E to minimally bound both MBRs A...

Write a function that takes a string as an input parameter and reverses the string. Validate the function by taking an input from the user and invoking the function.

A company borrowed $45,000 for 3 years at 5% compounded monthly. It will NOT make any payments on this loan prior to maturity. (a) Find the total future value the company will need to accumulate to...