Consider examples 9.2 and 9.3. Assume that social damage is quadratic as in the examples. Following section 9.2.3, assume that the regulator can only set a uniform tax. Determine the formula for the second-best optimal tax rate.

Data from example 9.2

example 9.3

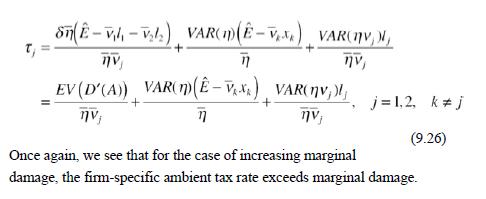
Data from section 9.2 .3

Example 9.2 (Numerical/Analytical) Suppose there are two firms with abatement cost functions C(1)=cl/2 and emissions e-(e-vlj), where e; is the maximum (unregulated) emission level, and and determine the effectiveness of abatement 1/1 activities 1 and 12, respectively. Denote =+ as the aggregate unregulated emission level, and let ambient pollution be given by A=n (e+)=n (E-vl-22), where n represents the aggregate uncertainty. We consider two damage functions, given by D(4A)=8.4 and D(4)=84/2, which represent constant and increasing marginal damages, respectively. The random variables (,2,n) are jointly distributed with independence as a special case, and we have d./de-n and defalvj. For the case of constant marginal damage we have D'(4)=6. According to Eq. (9.8), the first-order condition with constant marginal damage is cl = SEV (nv) = 8nv + SCOV (n. v), (9.10) where = EV(1) and V = EV(v) are the means of the random variables, and the constant marginal damage & is deterministic. From this expression, it is apparent that if n and v; are positively correlated, so that a large positive shock to ambient pollution is likely to accompany a high