Repeat Problem 7 but now use a dynamic allocation strategy such as Algorithm 31. Data given in

Question:

Repeat Problem 7 but now use a dynamic allocation strategy such as Algorithm 31.

Data given in Problem 7

Implement Algorithm 30 on the investment of Problem 2. Show the fortune after 30 iterations of the strategy, after 60. Estimate the mean and variance of these ending fortunes. Use at least 10,000 trials.

Data given in Algorithm 30

Fortune 1; f =0.145; gain = 0.88 for i=1 to N wager = f*Fortune U U (0,1) if U < 0.6 Fortune else Fortune

Data given in Algorithm 31

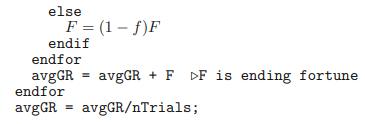
Data given in Problem 2

In Table 5.1 the second line gives the gain expectation for buying ATM calls as 0.161 with the probability of a gain as 0.37. Assuming complete loss of investment is the complementary probability, what is the average return on this investment? What is the size of the Kelly bet?

Data given in table 5.1

Table 5.11 Gain expectation for put and call options for the calls: So $80, T20(days), = 8%, r= 1%, o = 20%