The Gamma distribution, G(, ) has density given by Here () is the gamma function of Section 6.8 and equals (1)! if is a

The Gamma distribution, G(α, λ) has density given by

Here Γ(α) is the gamma function of Section 6.8 and equals (α−1)! if α is a positive integer. Show that the Gamma is infinitely divisible (empirically) by showing that the histogram for the sum of six samples of G(1, λ) has the same density as G(6, λ). Note that, for α a positive integer, then

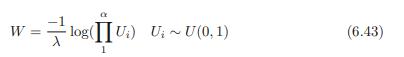
is a sample from G(α, λ),

fa(x: a, A) = 1a I(a)" --, x>0. -Ar (6.42)