Consider an exponential utility function 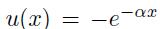, with a strictly positive . An investor characterised by this exponential utility has to allocate an initial wealth \(W_{0}\) between a risk-free and a risky asset. We assume a binomial uncertainty model, so that the risky asset has two possible gains (not returns) \(R_{u}\) and \(R_{d}\), with probabilities \({ }_{u}\) and \({ }_{d}\), respectively. Let \(q\) be the wealth allocated to the risky asset; it is possible to borrow cash as well to short-sell the risky asset. How does \(q\) change as a function of initial wealth \(W_{0}\) ? Do you think that your utility function is exponential?

u(x) -ax = -e