Let (u: mathbb{R} ightarrow mathbb{R}) be a twice differentiable utility function and denote by (r_{u}^{a}(x)) the coefficient of absolute risk aversion. Show that, for

Let \(u: \mathbb{R} \rightarrow \mathbb{R}\) be a twice differentiable utility function and denote by \(r_{u}^{a}(x)\) the coefficient of absolute risk aversion. Show that, for suitable 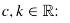\[u^{\prime}(x)=k \mathrm{e}^{-\int_{c}^{x} r_{u}^{a}(y) \mathrm{d} y}, \quad \text { for every } x \in \mathbb{R} .\]

c, k R: