Let \(f: \mathbb{R} ightarrow \mathbb{R}\) be a bounded increasing function. Show that \(f^{\prime}\) exists Lebesgue a.e. and \(f(b)--f(a) \geqslant \int_{(a, b)} f^{\prime}(x) d x\). When do we have equality?

[ assume first that \(f\) is left- or right-continuous. Then you can interpret \(f\) as the distribution function of a Stieltjes measure \(\mu\). Use Lebesgue's decomposition theorem to write \(\mu=\mu^{\circ}+\mu^{\perp}\) and use Corollaries 25.21 and 25.22 to find \(f^{\prime}\). If \(f\) is not one-sided continuous in the first place, use Lemma 14.14 to find a version \(\phi\) of \(f\) which is left- or right-continuous such that \(\{\phi eq f\}\) is at most countable, and hence a Lebesgue null set.]

Data from corollaries 25.21

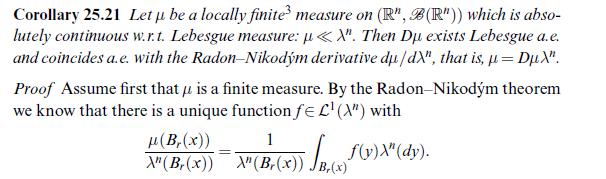
Data from corollary 25.22

Data from lemma 14.14

Corollary 25.21 Let u be a locally finite measure on (R", B(R")) which is abso- lutely continuous w.r.t. Lebesgue measure: u