Let us consider two zero-coupon bonds, whose issuers may default with probability \(4 \%\) (over some time horizon that we leave implicit). Say that, in the case of default, we lose the full face value, \(\$ 100\) (in practice, we might partially recover the face value of the bond). Let us compute the V@R of each bond with confidence level 95%. We represent the loss for the two bonds by random variables \(X\) and \(Y\), respectively, which take values in the set 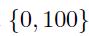 . Since loss has a discrete distribution in this example, we should use the more general definition of \(\mathrm{V} @ \mathrm{R}\) provided by the generalized inverse. The probability of default is \(4 \%\), and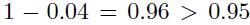; therefore, we find

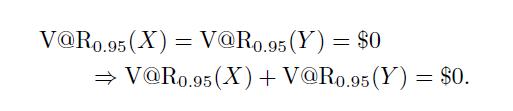
Now what happens if we hold both bonds and assume independent defaults? We will suffer:

- A loss of \(\$ 0\), with probability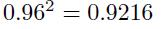

- A loss of \(\$ 100\), with probability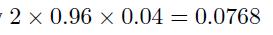

- A loss of \(\$ 200\), with probability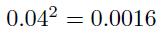

Now the probability of losing \(\$ 0\) is smaller than \(95 \%\), and

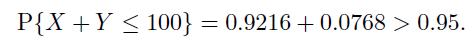
Hence, with that confidence level,

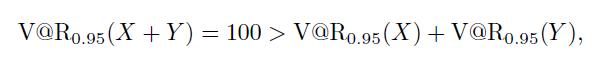
which means that risk, as measured by \(\mathrm{V} @ \mathrm{R}\), may be increased by diversification.

{0, 100}