Question: Compute the matrix exponential e At for each system x' = Ax given in Problems 9 through 20. x' 1 = 13x 1 + 4x
Compute the matrix exponential eAt for each system x' = Ax given in Problems 9 through 20.
x'1 = 13x1 + 4x2, x'2 = 4x1 + 7x2
Data in Problem 9 through 20
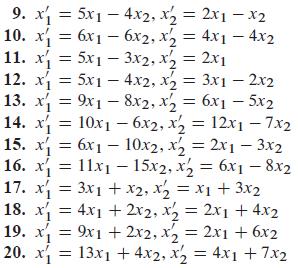
9. x = 5x14x2, x = 2x1-x2 x = 4x14x2 10. x = 6x16x2, x/2 11. x = 5x13x2, x = 2x1 12. x = 5x1 - 4x2, x = 3x1 - 2x2 13. x = 9x18x2, x = 6x1 - 5x2 14. x = 10x6x2, x = 12x1 - 7x2 15. x6x110x2, x2 = 2x13x2 16. x = 11x - 15x2, x = 6x1 - 8x2 17. x = 3x1 + x2, x = x + 3x 18. x = 4x1 + 2x2, x = 2x1 +4x2 X2 19. x = 9x1 + 2x2, x = 2x1 + 6x2 20. x 13x + 4x2, x = 4x1 + 7x2
Step by Step Solution
3.30 Rating (159 Votes )
There are 3 Steps involved in it
To compute the matrix exponential e At where A is the coefficient matrix of the system xAx we follow these steps Diagonalize matrix A if possible Compute e At using the diagonalized form of A if available To find the corresponding eigenvectors we substitute each eigenvalue back into AIX0 and solve for X We can express matrix A in terms of its eigenvectors and eigenvalues The diagonalization of A is given by Lets compute each part This is the matrix exponential for the given system If you have a specific value of t you can substitute it into this expression to get the numerical value of e At Given the system x ... View full answer

Get step-by-step solutions from verified subject matter experts


