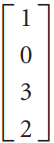
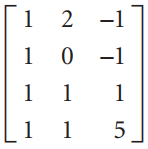
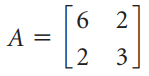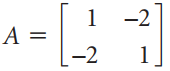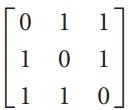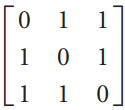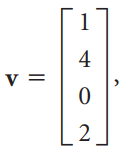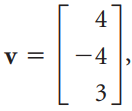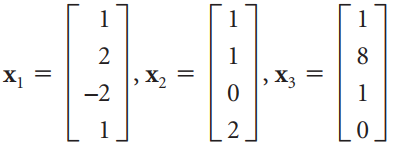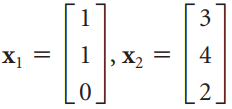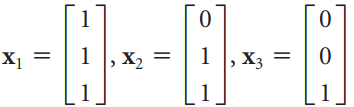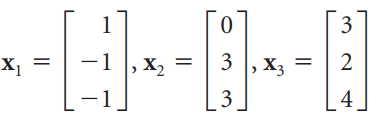Linear Algebra A Modern Introduction 3rd edition David Poole - Solutions
Discover a comprehensive resource for "Linear Algebra: A Modern Introduction, 3rd Edition" by David Poole. Access the answers key and solutions PDF, providing step-by-step answers to the textbook's challenging questions and answers. Our solution manual offers solved problems and chapter solutions that align with the instructor manual, ensuring a thorough understanding of the material. Enhance your learning with our test bank and free download options, offering valuable insights for both students and educators. Embrace the convenience of online solutions and elevate your grasp of linear algebra concepts today.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


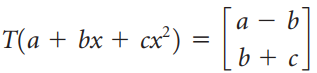

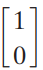
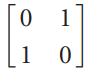
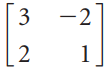
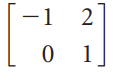

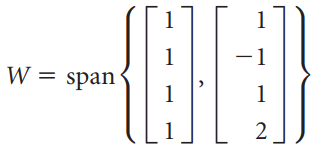
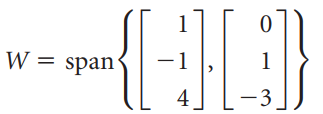
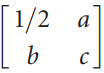
![6/7 -1/V5 _ 4/7V5 -15/7V5 2/7V5] 2/7 3/7 2/V5](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/0/6/9/2485b8e8e80b2b8f1536051572200.jpg)
![A = | 0 Lo 3 1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/9/9/2/6735b8d63615d53d1535974992346.jpg)
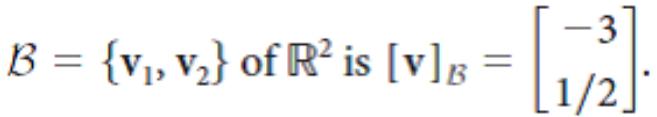
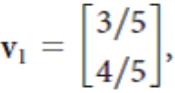
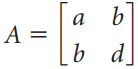
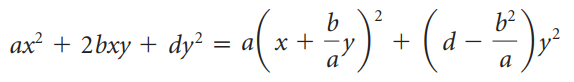

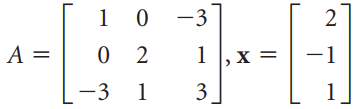
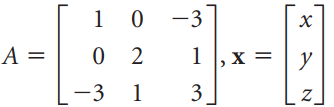

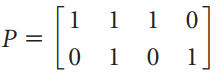
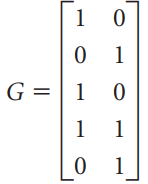
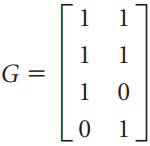

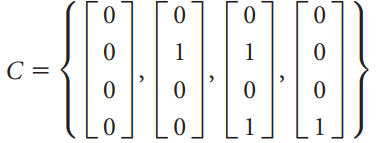
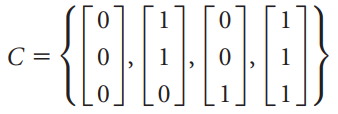
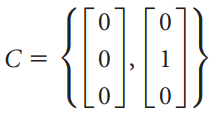
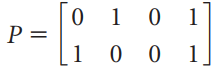

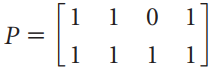
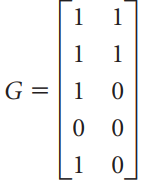
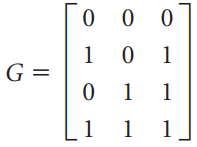
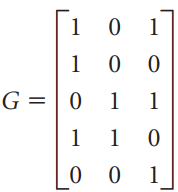
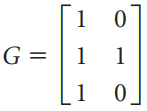
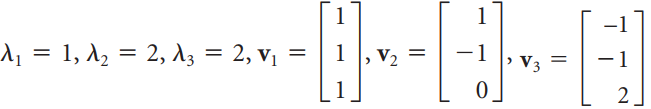

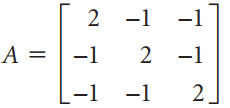
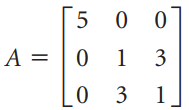

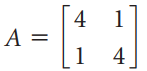
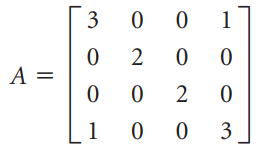
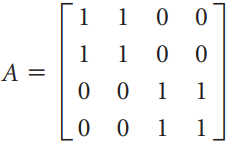
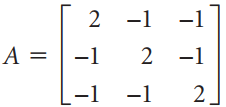
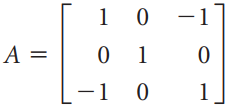
![[1 0 A = | 0 2] 4 2 [ 2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/9/9/2/7165b8d638c4b0c51535975035266.jpg)