First solve Eqs. (16) and (17) for e^-t and e^2t in terms of x(t), y(t), and the constants A and B. Then substitute the results in (e^2t) (e^-t)² = 1 to show that the trajectories of the system x' = y, y' = 2x + y in Example 6 satisfy an equation of the form

Then show that C = 0 yields the straight lines y = -x and y = 2x that are visible in Fig. 7.1.6.

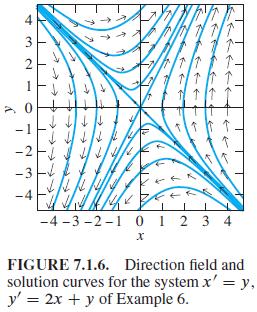
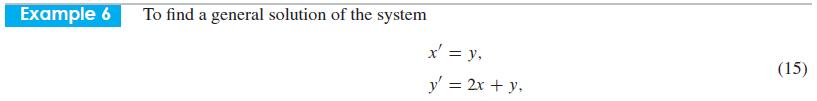
4x33xy + y = C (constant).