Question: In each of Problems 12 through 16, a second-order equation of the form x'' + f (x, x') = 0, corresponding to a certain mass-and-spring

In each of Problems 12 through 16, a second-order equation of the form x'' + f (x, x') = 0, corresponding to a certain mass-and-spring system, is given. Find and classify the critical points of the equivalent first-order system.

x'' + 2x' + 20x - 5x³ = 0: Verify that the critical points resemble those shown in Fig. 9.4.6.

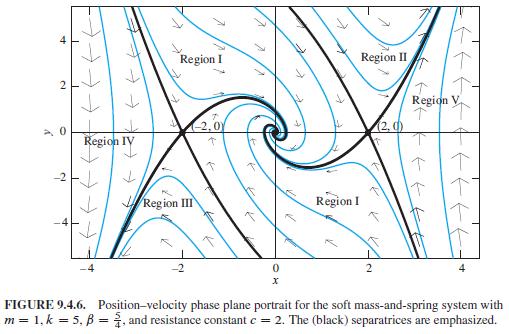
0 Region ly Region I Region III Region I Region II 2

0 Region ly Region I Region III Region I Region II 2 (2,0) Region V FIGURE 9.4.6. Position-velocity phase plane portrait for the soft mass-and-spring system with m = 1, k = 5, B = 4, and resistance constant c = 2. The (black) separatrices are emphasized.

Step by Step Solution

★★★★★

3.34 Rating (175 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Jx y 1 4 0 15x202 0 1 20 2 At 00 The Jacobian matrix J has characteristic equ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related First Course Differential Equations Questions!

Find the court decision located at 2007-1 USTC 50,210. a. Which court heard the case? b. Who was the judge(s)? c. Which tax year(s) is in question and in what year was the case decided? d. Which...

Please solve question 12 and 14 a In each of Problems 12 through 16, a second-order equation of the form x" + f(x,x') = 0, corresponding to a certain mass-and-spring system, is given. Find and...

Please answer these four questions. Apply the method of undetermined coefficients to find the particular solution to the following system that satisfies the given initial conditions. x' = 2x + 4y +...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

3 Systems of differential equations In Sections 3.8-3.10 we will reduce the problern of finding all solutions of (1) to the much simpler algebraic problern of solving simultaneous linear equations of...

You have been provided with the description of a programming language, J, intended for scripting applications. Its syntax is similar to a cut-down version of Java in that it consists of function...

A flat-plate solar collector consisting of an absorber plate and single cover plate, is inclined at an angle of T = 60 relative to the horizontal. Consider conditions for which the incident solar...

Calculate the retained earnings balance at the end of Year 2. Year 1 retained earnings at start of year 270.0 Year 1 net income 56.0 Year 1 dividend paid 29.0 Year 2 net income 73.0 Year 2 dividend...

8. Maintainability is the ease with which a product can be repaired or maintained.

What is an escalation clause, and how is it used in the construction contract?

The manager of a large shopping center in Buffalo is in the process of deciding on the type of snow clearing service to hire for his parking lot. Two services are available. The White Christmas...

Refer to Exercise 22.9. Using subjective assessments the manager has assigned the following probabilities to the number of snowfalls. Determine the optimal decision. P(0) = .05 P(1) = .15 P(2) = .30...

The owner of a clothing store must decide how many mens shirts to order for the new season. For a particular type of shirt, she must order in quantities of 100 shirts. If she orders 100 shirts, her...

Discuss the differences between the Cost of Goods Sold (COGS) in a manufacturing operation versus a retail type operation. Are there any manufacturing type operations in Hawaii that you know of and...

Use the following bank statement and T-account to prepare the May 31 bank reconciliation. BANK STATEMENT Deposits Checks Other $ 65 Date May 1 4 12 28 30 May 31 NSF check $65 #2 #4 #5 #6 #8 $ 25 115...

Valber Company is considering eliminating its phone division. The company allocates fixed costs based on sales. If the phone division is dropped, S161,000 of the fixed costs allocated to that...