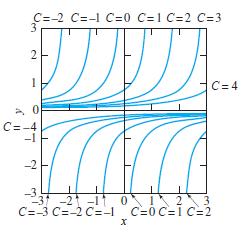
In Example 7 we saw that y(x) = 1/(C - x) defines a one-parameter family of solutions of the differential equation dy/dx = y².

(a) Determine a value of C so that y (10) = 10.

(b) Is there a value of C such that y(0) = 0? Can you nevertheless find by inspection a solution of dy/dx = y² such that y(0) = 0?

(c) Figure 1.1.8 shows typical graphs of solutions of the form y(x) = 1/(C - x). Does it appear that these solution curves fill the entire xy- plane? Can you conclude that, given any point (a, b) in the plane, the differential equation dy/dx = y² has exactly one solution y(x) satisfying the condition y(a) = b?

FIGURE 1.1.8. Graphs of solutions of the equation dy/dx = y².

Example 7

C=-2 C=-1 C=0 C=1 C=2 C=3 2 1 0 C=-4 -1 -2 -3 -2 -11 01 C=-3 C=-2 C=-1 2 3 C=0C-16=2 X C=4