Equilibria, Phase Lines and Bifurcations

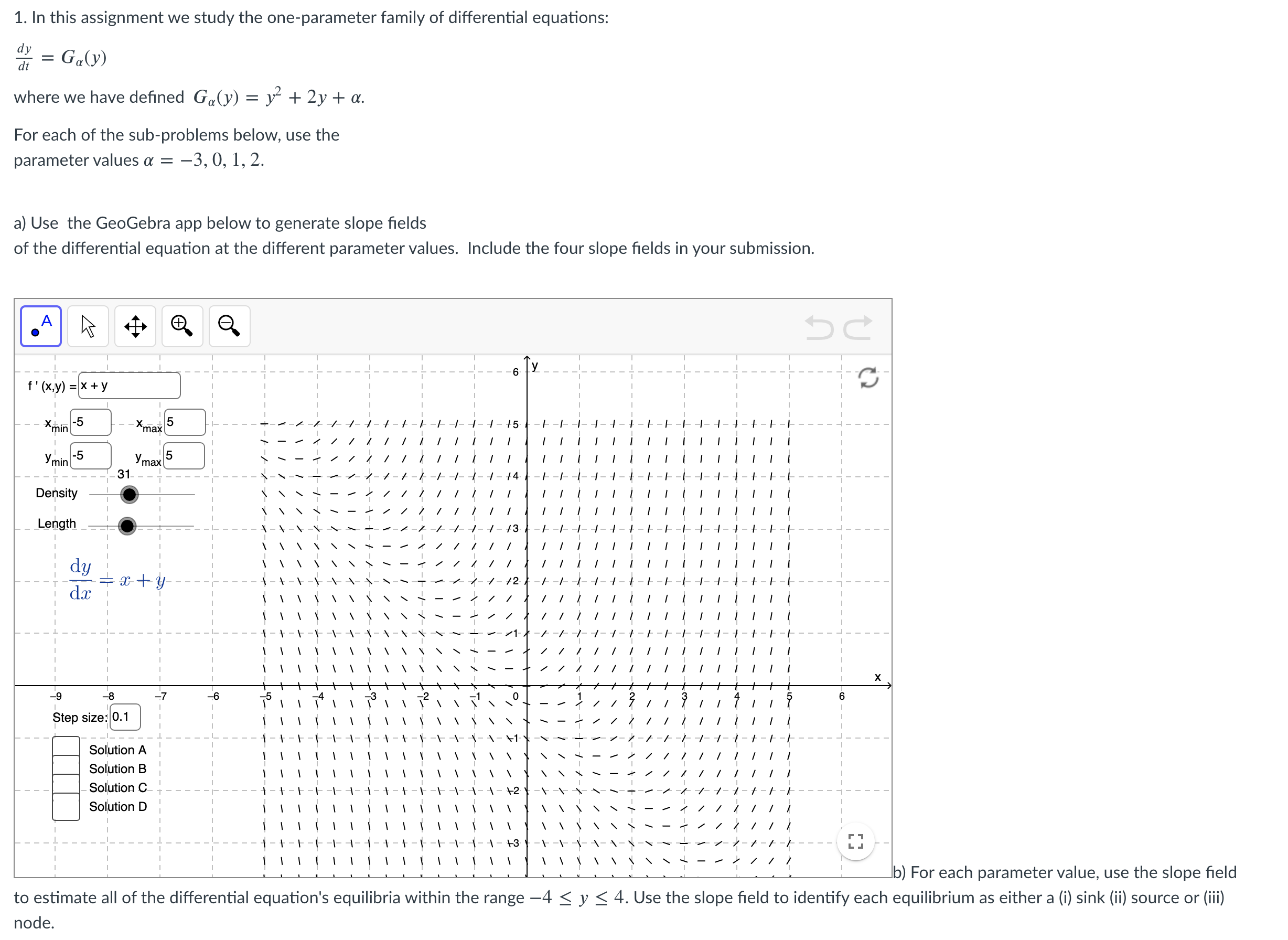
1. In this assignment we study the one-parameter family of differential equations: dy = Ga(y) where we have defined Ga(y) = y- + 2y + a. For each of the sub-problems below, use the parameter values a = -3, 0, 1, 2. a) Use the GeoGebra app below to generate slope fields of the differential equation at the different parameter values. Include the four slope fields in your submission. A f ' ( x, y ) = x + y * min :5 Xmax - 1 - 45 min max 31- -4-1-1 -1-4 Density Length dy dx -9 -8 -7 -6 6 Step size: 0.1 Solution A Solution B Solution C Solution D b) For each parameter value, use the slope field to estimate all of the differential equation's equilibria within the range -4