Problems 43 through 46 concern the differential equation

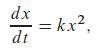
where k is a constant.

Suppose the velocity v of a motorboat coasting in water satisfies the differential equation dv/dt = kv². The initial speed of the motorboat is v(0) = 10 meters per second (m/s), and v is decreasing at the rate of 1 m/s² when v = 5 m/s. Based on the result of Problem 43, long does it take for the velocity of the boat to decrease to 1 m/s? To 1/10m/s? When does the boat come to a stop?

dx dt = kx2,