Verify that if c is a constant, then the function defined piecewise by

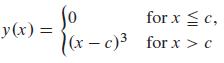
satisfies the differential equation y' = 3y^2/3 for all x. Can you also use the "left half" of the cubic y = (x - c)³ in piecing together a solution curve of the differential equation? (See Fig. 1.3.25.) Sketch a variety of such solution curves. Is there a point (a, b) of the xy-plane such that the initial value problem y' = 3y^2/3, y(a) = b has either no solution or a unique solution that is defined for all x? Reconcile your answer with Theorem 1.

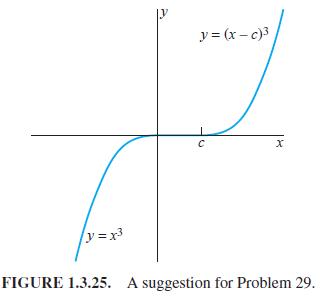
y(x) = (x-c) for x c, for x > c.