A Taylor series expansion of function f(x) about some x-location x0 is given as

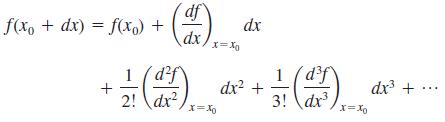
Consider the function f(x) = exp(x) = e^x. Suppose we know the value of f(x) at x = x₀, i.e., we know the value of f(x₀), and we want to estimate the value of this function at some x location near x₀. Generate the first four terms of the Taylor series expansion for the given function (up to order dx³ as in the above equation). For x₀ = 0 and dx = –0.1, use your truncated Taylor series expansion to estimate f(x₀ + dx). Compare your result with the exact value of e^-0.1. How many digits of accuracy do you achieve with your truncated Taylor series?

Transcribed Image Text:

f(xo + dx) = f(x) + df dx X = Xo 1 +(2)... 2! dx² dx dx² + + 1 3! d³f\ dx³ X = Xo dx³ +