Paul realizes that the pump being used in Prob. 14–39E is not well-matched for this application, since its shutoff head (125 ft) is much larger than its required net head (less than 30 ft), and its capacity is fairly low. In other words, this pump is designed for high-head, low-capacity applications, whereas the application at hand is fairly low-head, and a higher capacity is desired. Paul tries to convince his supervisor that a less expensive pump, with lower shutoff head but higher free delivery, would result in a significantly increased flow rate between the two reservoirs. Paul looks through some online brochures, and finds a pump with the performance data shown in Table P14–42E. His supervisor asks him to predict the volume flow rate between the two reservoirs if the existing pump were replaced with the new pump. 

(a) Perform a least-squares curve fit (regression analysis) of H_available versus V̇², and calculate the best-fit values of coefficients H₀ and a that translate the tabulated data of Table P14–42E into the parabolic expression H_available = H₀ – aV̇². Plot the data points as symbols and the curve fit as a line for comparison. 

(b) Estimate the operating volume flow rate of the new pump if it were to replace the existing pump, all else being equal. Compare to the result of Prob. 14–39E and discuss. Is Paul correct? 

(c) Generate a plot of required net head and available net head as functions of volume flow rate and indicate the operating point on the plot.

Data from Problem 14–39E

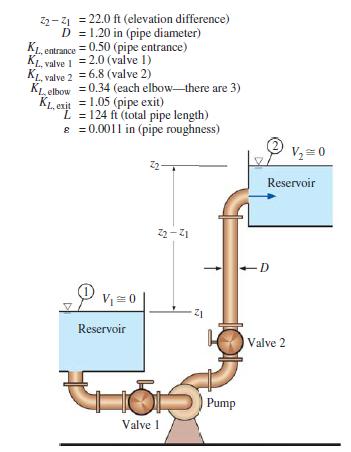
A water pump is used to pump water from one large reservoir to another large reservoir that is at a higher elevation. The free surfaces of both reservoirs are exposed to atmospheric pressure, as sketched in Fig. P14–39E. The dimensions and minor loss coefficients are provided in the figure. The pump’s performance is approximated by the expression H_available = H₀ – aV̇², where the shutoff head H₀ = 125 ft of water column, coefficient a = 2.50 ft/gpm², available pump head H_available is in units of feet of water column, and capacity V̇ is in units of gallons per minute (gpm). Estimate the capacity delivered by the pump.

FIGURE P14–39E

Transcribed Image Text:

22-21 = 22.0 ft (elevation difference) D 1.20 in (pipe diameter) KL, entrance = 0.50 (pipe entrance) = 2.0 (valve 1) =6.8 (valve 2) KL, valve 1 KL, valve 2 KL. elbow = 0.34 (each elbow-there are 3) KL, exit = 1.05 (pipe exit) L=124 ft (total pipe length) 8 = 0.0011 in (pipe roughness) V₁=0 Reservoir 22- 22-21 Valve 1 Z1 <-D Pump Reservoir V/₂=0 Valve 2