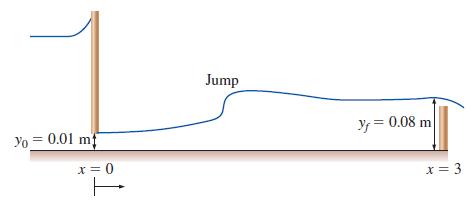
While the GVF equation cannot be used to predict a hydraulic jump directly, it can be coupled with the ideal hydraulic jump depth ratio equation in order to help locate the position at which a jump will occur in a channel. Consider a jump created in a wide (R_h ≈ y) horizontal (S₀ = 0) laboratory flume having a length of 3m and a Manning coefficient of 0.009. The supercritical flow under the head gate has an initial depth of 0.01 m at x = 0. The tailgate results in an overflow depth of 0.08 m at x = 3 m. The perunit-width flow rate is 0.025m³/s·m. 

(a) Calculate the critical depth of the flow and verify that the initial and final flows are supercritical and subcritical, respectively. 

(b) Determine the location of the hydraulic jump. 

Integrate the GVF equation from x = 0 to a “guessed” location of the jump, apply the jump depth-ratio equation, and integrate the GVF equation using this new initial condition from the jump location to x = 3 m. If you do not obtain the desired overflow depth, try a new jump location.

FIGURE P13–92

Yo= 0.01 m x = 0 Jump = 0.08 m x = 3