Following the guidance in Secs. 13.2 and 13.3, lay out in detail a plan of attack for the solution of the supersonic flow over a right-circular cone at an angle of attack low enough so that the shock wave is attached to the vertex.

Guidelines From Section 13.2 & 13.3:

1. The flow-field shown in Fig. 13.3 is a function of two independent variables, \(\theta\) and \(\phi\), in contrast to the zero- \(\alpha\) case where \(\theta\) is the only independent variable.

Figure 13.3:

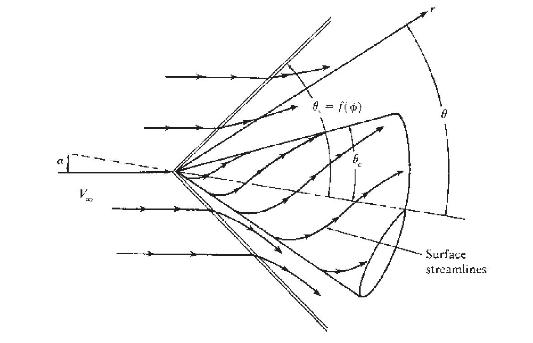
2. The shock wave angle \(\theta_{s}\) is different for each meridional plane, i.e., \(\theta_{s}\) is a function of \(\phi\).
3. The streamlines along the cone surface are now curved streamlines which curl around the body from the bottom of the cone (called the windward surface) to the top of the cone (called the leeward surface). However, each of the curved streamlines along the surface emanates from the vertex of the cone. Only two surface streamlines are straight-those along the very top and bottom rays.
4. The streamlines in the flow between the shock wave and the body are no longer planar; they are curved in the three-dimensional space between the shock and the body.
5. Because the flow is adiabatic and inviscid, the entropy is constant along a given streamline between the shock and the body. However, streamlines that pass through different points on the shock wave experience different increases in entropy across the shock, because the shock wave angle \(\theta_{s}\) is different. Hence, the flow between the shock and the body has finite gradients in entropy perpendicular to the streamlines. An important consequence of these entropy gradients is that the flow is rotational, as seen from Crocco's theorem, given by Eq. (6.60). In this sense, the supersonic flow over a cone at angle of attack is analogous to the flow over a supersonic blunt body.

\[\begin{equation*}
\frac{p_{\mathrm{A}} p_{\mathrm{B}}}{p_{\mathrm{AB}}}=K_{p}(T) \tag{16.60}
\end{equation*}\]

Transcribed Image Text:

V Surface streamlines