Solve the following LP problem using the appropriate algorithm

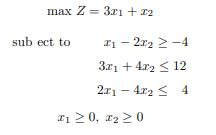
a) Exhibit the complete primal and dual solutions. Recalculate the optimal value of the primal and the dual ob ective functions.

b) Exhibit the optimal primal feasible basis and its inverse.

c) Verify that the product of the optimal basis and its inverse results in the identity matrix.

d) Write down the dual problem and identify the optimal dual feasible basis using the information contained in the last row of the optimal tableau.

e) Verify that the dual variables can be obtained also by multiplying the row vector of revenue coefficients associated with basic activities by the inverse of the optimal basis (Place the row vector of the revenue coefficients in front of the inverse matrix).

f) Verify that the primal basic solution can be obtained by multiplying the inverse of the optimal basis by the column vector of right-hand-side (RHS) coefficients (Place the column vector of RHS coefficients after the inverse matrix).
g) State the two sets of complementary slackness conditions of the Equilibrium Problem.
h) Verify the complementary slackness conditions with the results of the optimal tableau.

sub ect to max Z=3x1 + x2 21-22-4 3x1 + 4x2 12 2x14x24 1 0, 20