The following problem is an example of an unbounded LP problem. This means that one of the coordinates of the optimal solution can achieve the value of positive infinity. This happens because, at a certain stage, all the coefficients of the incoming activity are either zero or negative. In other words, it is not possible to find a pivot element for that tableau. Given the following LP problem

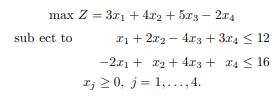
a) Solve the above problem using the primal simplex algorithm and show that the problem is unbounded and, therefore, has no finite optimal solution.

b) Note that, in order to eliminate the unboundedness of the previous LP problem, it is sufficient to change one coefficient of activity 1. Given the following LP problem

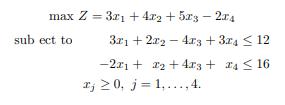
c) Solve the above problem using the primal simplex algorithm and exhibit all the elements of the primal optimal solution and of the dual optimal solution.

d) Recalculate the value of all the components of the dual optimal solution using the notion (and the formula) of opportunity cost. In particular, show that the opportunity cost of activity 2 is z2 − c2 = 55/4; the opportunity cost of activity 4 is z4 − c4 = 101/4; the opportunity cost (VMP1) of input 1 is y1 = zs1 − cs1 = 11/2; and the opportunity cost (VMP2) of input 2 is y2 = zs2 − cs2 = 27/4.

e) By how much should the price of activity 2 be increased before it becomes a profitable activity?

f) By how much should the price of activity 4 be increased before it becomes a profitable activity?

max Z=3x+4x2+5x3 - 2x4 sub ect to - 1+222 423 +34 12 -2x1+2+4x3 + 24 16 x; 0, j=1,...,4.