Let \(\widehat{A}\) be a double-centered distance matrix. Prove or disprove the following statements:

1. If \(B\) is the matrix obtained by double-centering \(\widehat{A}\), then \(B=\widehat{A}\).

2. If \(c\) is a constant and \(B\) denotes the matrix obtained by adding \(c\) to the off-diagonal elements of \(\widehat{A}\), then \(\widehat{B}=\widehat{A}\).

Compare your conclusions to Lemma 17.1.

Data from Lemma 17.1

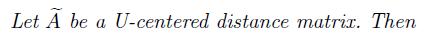
Let A be a U-centered distance matrix. Then