Solve the following initial value problem for u(x, ) on a semi-infinite interval, using a Greens function: with u(x, 0) = u 0 (x)

Solve the following initial value problem for u(x, τ ) on a semi-infinite interval, using a Green’s function:

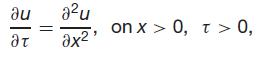
with
u(x, 0) = u₀(x) for x > 0, u(0, τ ) = 0 for τ > 0.

Define v(x, τ) as

v(x, τ ) = u(x, τ) if x > 0,
v(x, τ ) = −u(−x, τ) if x

Then we can show that v(0, τ ) = 0 and

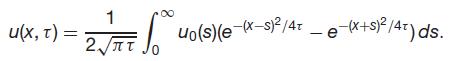
a2u on x > 0, t > 0, au ax2 *