Consider a solid circular shaft of length \(L\) and radius \(c\) made of an elastoplastic material whose shear stress-shear strain diagram is shown in Figure P2.15(a). If the applied torque is such that the shear stress at the outer radius of the shaft is less than \(\tau_{p}\), a linear relationship between the torque and the angular displacement exists. When the applied torque is large enough to cause plastic behavior, a plastic shell is developed around an elastic core of radius \(r

(a) The shear strain at the outer radius of the shaft is related to the angular displacement \(\theta=\frac{\gamma_{c} L}{c}\). The shear strain distribution is linear over a given cross section. Show that this implies

\[ \theta=\frac{L \tau_{P}}{r G} \]

(b) The torque is the resultant moment of the shear stress distribution over the cross section of the shaft,

\[ T=\int_{0}^{c} 2 \pi \tau ho^{2} d ho \]

Use this to relate the torque to the radius of the elastic core.

(c) Determine the relationship between \(\delta T\) and \(\delta \theta\).

(d) Approximate the stiffness of the shaft by a linear torsional spring. What is the equivalent torsional stiffness?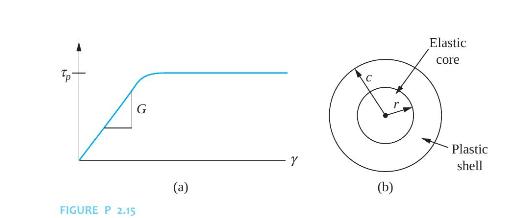

G (a) FIGURE P 2.15 Elastic core Plastic shell