Consider an ordinary binary search tree augmented by adding to each node x the attribute x.size giving the number of keys stored in the subtree rooted at x. Let ? be a constant in the range 1/2 ? ?

a.?A?1/2-balanced tree is, in a sense, as balanced as it can be. Given a node?x?in an arbitrary binary search tree, show how to rebuild the subtree rooted at?x?so that it becomes?1/2-balanced. Your algorithm should run in time??(x.size), and it can use?O(x.size)?auxiliary storage.

b.?Show that performing a search in an?n-node??-balanced binary search tree takes?O(lg?n)?worst-case time.

For the remainder of this problem, assume that the constant???is strictly greater than?1/2. Suppose that we implement INSERT?and DELETE?as usual for an?n-node binary search tree, except that after every such operation, if any node in the tree is no longer??-balanced, then we "rebuild" the subtree rooted at the highest such node in the tree so that it becomes?1/2-balanced.

We shall analyze this rebuilding scheme using the potential method. For a node x in a binary search tree T, we define ?(x) = |x.left.size - x.right.size|, and we define the potential of T as

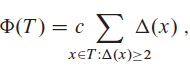
where?c?is a sufficiently large constant that depends on??.

c. Argue that any binary search tree has nonnegative potential and that a 1/2-balanced tree has potential 0.

d.?Suppose that?m?units of potential can pay for rebuilding an?m-node subtree. How large must?c?be in terms of???in order for it to take?O(1)?amortized time to rebuild a subtree that is not??-balanced?

e. Show that inserting a node into or deleting a node from an n-node ?-balanced tree costs O(lg n) amortized time.

() (), xeT:A(x)>2