In this problem, we prove that the average depth of a node in a randomly built binary search tree with n nodes is O(lg n). Although this result is weaker than that of Theorem 12.4, the technique we shall use reveals a surprising similarity between the building of a binary search tree and the execution of RANDOMIZED QUICKSORT from Section 7.3.

We define the total path length P(T) of a binary tree T as the sum, over all nodes x in T, of the depth of node x, which we denote by d(x, T).

Figure 12.5 A radix tree storing the bit strings 1011, 10, 011, 100, and 0. We can determine each node€™s key by traversing the simple path from the root to that node. There is no need, therefore, to store the keys in the nodes; the keys appear here for illustrative purposes only. Nodes are heavily shaded if the keys corresponding to them are not in the tree; such nodes are present only to establish a path to other nodes.

a. Argue that the average depth of a node in T is

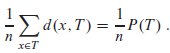
Thus, we wish to show that the expected value of P(T) is O(n lg n).

b. Let T_L and T_R denote the left and right subtrees of tree T, respectively. Argue that if T has n nodes, then

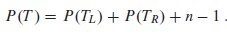
c. Let P(n) denote the average total path length of a randomly built binary search tree with n nodes. Show that

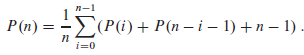
d. Show how to rewrite P(n) as

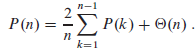
e. Recalling the alternative analysis of the randomized version of quicksort given in Problem 7-3, conclude that P(n) = O(n lg n).

At each recursive invocation of quicksort, we choose a random pivot element to partition the set of elements being sorted. Each node of a binary search tree partitions the set of elements that fall into the subtree rooted at that node.

f. Describe an implementation of quicksort in which the comparisons to sort a set of elements are exactly the same as the comparisons to insert the elements into a binary search tree. (The order in which comparisons are made may differ, but the same comparisons must occur.)

10 011 100 1011 -P(T) -(, T) (T) . ET