For a given polygon P and a point q on its boundary, the shadow of q is the set of points r such that the segment q̅r is entirely on the boundary or in the interior of P. As Figure 33.10 illustrates, a polygon P is star-shaped if there exists a point p in the interior of P that is in the shadow of every point on the boundary of P. The set of all such points p is called the kernel of P. Given an n-vertex,  

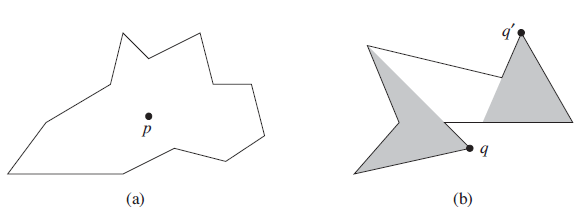
Figure 33.10 The definition of a star-shaped polygon, for use in Exercise 33.3-4. (a) A star-shaped polygon. The segment from point p to any point q on the boundary intersects the boundary only at q. (b) A non-star-shaped polygon. The shaded region on the left is the shadow of q, and the shaded region on the right is the shadow of q′. Since these regions are disjoint, the kernel is empty. star-shaped polygon P specified by its vertices in counterclockwise order, show how to compute CH (P) in O(n) time.