If we insert a set of n items into a binary search tree, the resulting tree may be horribly unbalanced, leading to long search times. As we saw in Section 12.4, however, randomly built binary search trees tend to be balanced. Therefore, one strategy that, on average, builds a balanced tree for a fixed set of items would be to randomly permute the items and then insert them in that order into the tree.

What if we do not have all the items at once? If we receive the items one at a time, can we still randomly build a binary search tree out of them?

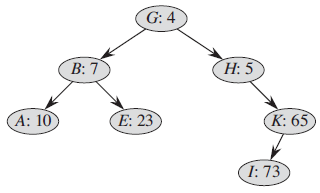
Figure 13.9 A treap. Each node x is labeled with x.key . x.priority. For example, the root has key G and priority 4. 

We will examine a data structure that answers this question in the affirmative. A treap is a binary search tree with a modified way of ordering the nodes. Figure 13.9 shows an example. As usual, each node x in the tree has a key value x.key. In addition, we assign x.priority, which is a random number chosen independently for each node. We assume that all priorities are distinct and also that all keys are distinct. The nodes of the treap are ordered so that the keys obey the binary-searchtree property and the priorities obey the min-heap order property.

If ν is a left child of u, then ν.key 

If ν is a right child of u, then ν.key > u.key.

If ν is a child of u, then ν.priority > u.priority.

(This combination of properties is why the tree is called a "treap". it has features of both a binary search tree and a heap.) 

It helps to think of treaps in the following way. Suppose that we insert nodes x₁, x₂, . . . ,x_n, with associated keys, into a treap. Then the resulting treap is the tree that would have been formed if the nodes had been inserted into a normal binary search tree in the order given by their (randomly chosen) priorities, i.e., x_i .priority j .priority means that we had inserted x_i before x_j.

a. Show that given a set of nodes x₁, x₂, . . . ,x_n, with associated keys and priorities, all distinct, the treap associated with these nodes is unique.

b. Show that the expected height of a treap is Θ(lg n), and hence the expected time to search for a value in the treap is Θ(lg n).

Let us see how to insert a new node into an existing treap. The first thing we do is assign to the new node a random priority. Then we call the insertion algorithm, which we call TREAP-INSERT, whose operation is illustrated in Figure 13.10.

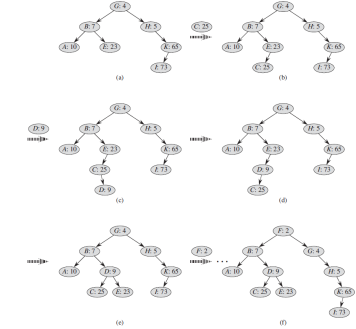
Figure 13.10 The operation of TREAP-INSERT. (a) The original treap, prior to insertion. (b) The treap after inserting a node with key C and priority 25. (c)–(d) Intermediate stages when inserting a node with key D and priority 9. (e) The treap after the insertion of parts (c) and (d) is done. (f) The treap after inserting a node with key F and priority 2.

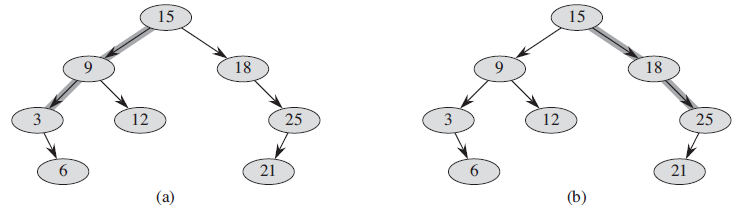
Figure 13.11 Spines of a binary search tree. The left spine is shaded in (a), and the right spine is shaded in (b). 

c. Explain how TREAP-INSERT works. Explain the idea in English and give pseudocode. Execute the usual binary-search-tree insertion procedure and then perform rotations to restore the min-heap order property.

d. Show that the expected running time of TREAP-INSERT is Θ(lg n). 

TREAP-INSERT performs a search and then a sequence of rotations. Although these two operations have the same expected running time, they have different costs in practice. A search reads information from the treap without modifying it. In contrast, a rotation changes parent and child pointers within the treap. On most computers, read operations are much faster than write operations. Thus we would like TREAP-INSERT to perform few rotations. We will show that the expected number of rotations performed is bounded by a constant. 

In order to do so, we will need some definitions, which Figure 13.11 depicts. The left spine of a binary search tree T is the simple path from the root to the node with the smallest key. In other words, the left spine is the simple path from the root that consists of only left edges. Symmetrically, the right spine of T is the simple path from the root consisting of only right edges. The length of a spine is the number of nodes it contains.

e. Consider the treap T immediately after TREAP-INSERT has inserted node x. Let C be the length of the right spine of the left subtree of x. Let D be the length of the left spine of the right subtree of x. Prove that the total number of rotations that were performed during the insertion of x is equal to C + D. 

We will now calculate the expected values of C and D. Without loss of generality, we assume that the keys are 1,2, . . . ,n, since we are comparing them only to one another. For nodes x and y in treap T, where y ≠ x, let k = x.key and i = y.key. We define indicator random variables X_ik = I {y is in the right spine of the left subtree of x}. 

f. Show that X_ik = 1 if and only if y.priority > x.priority, y.key

g. Show that

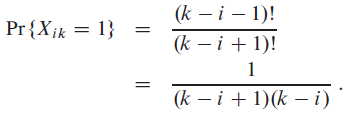
h. Show that

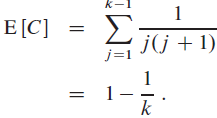
i. Use a symmetry argument to show that

j. Conclude that the expected number of rotations performed when inserting a node into a treap is less than 2.