In this problem, we give pseudocode for three different algorithms. Each one takes a connected graph and a weight function as input and returns a set of edges T. For each algorithm, either prove that T is a minimum spanning tree or prove that T is not a minimum spanning tree. Also describe the most efficient implementation of each algorithm, whether or not it computes a minimum spanning tree.

a.?MAYBE-MST-A?(G, w)

b. MAYBE-MST-B (G, w)

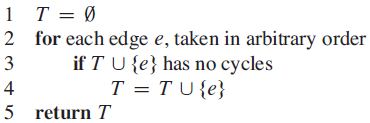
c. MAYBE-MST-C (G, w)

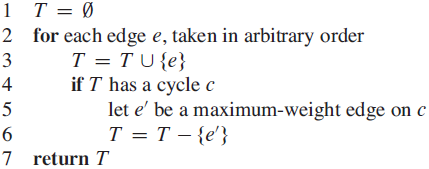
1 T = 2 for each edge e, taken in arbitrary order if T U {e} has no cycles T = TU {e} 4 5 return T