One class of permutations of the integers in the set S_n = {0, 1, 2, . . . , 2ⁿ − 1} is defined by matrix multiplication over GF (2). For each integer x in S_n, we view its binary representation as an n-bit vector

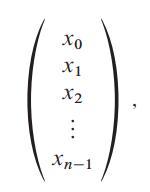
where

If A is an n × n matrix in which each entry is either 0 or 1, then we can define a permutation mapping each value x in S_n to the number whose binary representation is the matrix-vector product Ax. Here, we perform all arithmetic over GF (2): all values are either 0 or 1, and with one exception the usual rules of addition and multiplication apply. The exception is that 1 + 1 = 0. You can think of arithmetic over GF (2) as being just like regular integer arithmetic, except that you use only the least significant bit. As an example, for S₂ = {0, 1, 2, 3}, the matrix

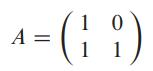
defines the following permutation μ_A: μ_A(0) = 0, μ_A (1) = 3, μ_A(2) = 2, μ_A(3) = 1. To see why μ_A(3) = 1, observe that, working in GF (2),

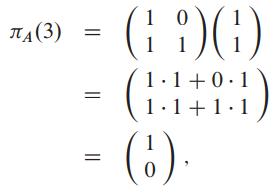
which is the binary representation of 1.

For the remainder of this problem, we work over GF (2), and all matrix and vector entries are 0 or 1. We define the rank of a 0-1 matrix (a matrix for which each entry is either 0 or 1) over GF(2) the same as for a regular matrix, but with all arithmetic that determines linear independence performed over GF(2). We define the range of an n × n 0-1 matrix A by

so that R (A) is the set of numbers in S_n that we can produce by multiplying each value x in S_n by A.

a. If r is the rank of matrix A, prove that |R (A)| = 2^r. Conclude that A defines a permutation on S_n only if A has full rank.

For a given n × n matrix A and a given value y ∈ (R.A), we define the preimage of y by

so that P (A, y) is the set of values in S_n that map to y when multiplied by A.

b. If r is the rank of n × n matrix A and y ∈ R (A), prove that |P (A, y)| = 2^n−r.

Let 0 ≤ m ≤ n, and suppose we partition the set S_n into blocks of consecutive numbers, where the ith block consists of the 2^m numbers i2^m, i2^m + 1, i2^m + 2, . . . , (i + 1)2^m − 1. For any subset S ⊆ S_n, define B (S, m) to be the set of size-2^m blocks of S_n containing some element of S. As an example, when n = 3, m = 1, and S = {1, 4, 5}, then B (S, m) consists of blocks 0 (since 1 is in the 0th block) and 2 (since both 4 and 5 are in block 2).

c. Let r be the rank of the lower left (n−m) × m submatrix of A, that is, the matrix formed by taking the intersection of the bottom n−m rows and the leftmost m columns of A. Let S be any size-2^m block of S_n, and let S' = {y : y = Ax for some x ∈ S}. Prove that |B (S' , m)| = 2^r and that for each block in B (S' , m), exactly 2^m−r numbers in S map to that block.

Because multiplying the zero vector by any matrix yields a zero vector, the set of permutations of S_n defined by multiplying by n × n 0-1 matrices with full rank over GF (2) cannot include all permutations of S_n. Let us extend the class of permutations defined by matrix-vector multiplication to include an additive term, so that x ∈ S_n maps to Ax + c, where c is an n-bit vector and addition is performed over GF (2). For example, when

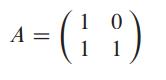
and

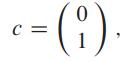
we get the following permutation π_{A, c} : π_{A, c} (0) = 2, π_{A, c} (1) = 1, π_{A, c} (2) = 0, π_{A, c} (3) = 3. We call any permutation that maps x ∈ S_n to Ax + c, for some n × n 0-1 matrix A with full rank and some n-bit vector c, a linear permutation.

d. Use a counting argument to show that the number of linear permutations of S_n is much less than the number of permutations of S_n.

e. Give an example of a value of n and a permutation of S_n that cannot be achieved by any linear permutation.

Transcribed Image Text:

и-1 х3 Li=o X;2'.