The binomial tree B_k is an ordered tree (see Section B.5.2) defined recursively.

As shown in Figure 19.6(a), the binomial tree B₀ consists of a single node. The binomial tree B_k consists of two binomial trees B_k-1 that are linked together so that the root of one is the leftmost child of the root of the other. Figure 19.6(b) shows the binomial trees B₀ through B₄.

a. Show that for the binomial tree B_k,

1. There are 2^k nodes,

2. The height of the tree is k,

3. There are exactly (^k_I) nodes at depth i for i = 0, 1, . . . , k, and

4. The root has degree k, which is greater than that of any other node, moreover, as Figure 19.6(c) shows, if we number the children of the root from left to right by k − 1, k − 2, . . . ,0, then child i is the root of a subtree B_i .

A binomial heap H is a set of binomial trees that satisfies the following properties.

1. Each node has a key (like a Fibonacci heap).

2. Each binomial tree in H obeys the min-heap property.

3. For any nonnegative integer k, there is at most one binomial tree in H whose root has degree k.

b. Suppose that a binomial heap H has a total of n nodes. Discuss the relationship between the binomial trees that H contains and the binary representation of n. Conclude that H consists of at most ⌊lg n⌋ + 1 binomial trees.

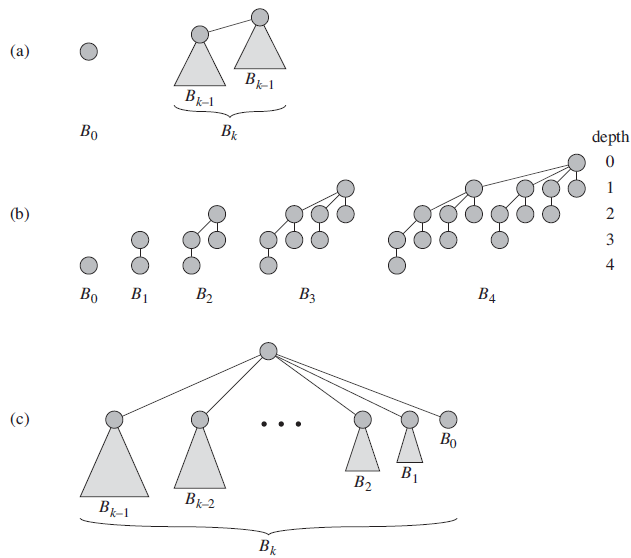
Figure 19.6 

(a) The recursive definition of the binomial tree B_k. Triangles represent rooted subtrees. (b) The binomial trees B₀ through B₄. Node depths in B₄ are shown. (c) Another way of looking at the binomial tree B_k.

Suppose that we represent a binomial heap as follows. The left-child, rightsibling scheme of Section 10.4 represents each binomial tree within a binomial heap. Each node contains its key, pointers to its parent, to its leftmost child, and to the sibling immediately to its right (these pointers are NIL when appropriate), and its degree (as in Fibonacci heaps, how many children it has). The roots form a singly linked root list, ordered by the degrees of the roots (from low to high), and we access the binomial heap by a pointer to the first node on the root list.

c. Complete the description of how to represent a binomial heap (i.e., name the attributes, describe when attributes have the value NIL, and define how the root list is organized), and show how to implement the same seven operations on binomial heaps as this chapter implemented on Fibonacci heaps. Each operation should run in O(lg n) worst-case time, where n is the number of nodes in the binomial heap (or in the case of the UNION operation, in the two binomial heaps that are being united). The MAKE-HEAP operation should take constant time.

d. Suppose that we were to implement only the mergeable-heap operations on a Fibonacci heap (i.e., we do not implement the DECREASE-KEY or DELETE operations).

How would the trees in a Fibonacci heap resemble those in a binomial heap? How would they differ? Show that the maximum degree in an n-node Fibonacci heap would be at most ⌊lg n⌋.

e. Professor McGee has devised a new data structure based on Fibonacci heaps. A McGee heap has the same structure as a Fibonacci heap and supports just the mergeable-heap operations. The implementations of the operations are the same as for Fibonacci heaps, except that insertion and union consolidate the root list as their last step. What are the worst-case running times of operations on McGee heaps?