Question: Let x be a binomial random variable with n = 20 and p = .1. a. Calculate P(x ¤ 4) using the binomial formula. b.

Let x be a binomial random variable with n = 20 and p = .1.

a. Calculate P(x ‰¤ 4) using the binomial formula.

b. Calculate P(x ‰¤ 4) using Table 1 in Appendix I.

c. Use the MINITAB output at the top of the page to calculate P(x ‰¤ 4). Compare the results of parts a, b, and c.

d. Calculate the mean and standard deviation of the random variable x.

e. Use the results of part d to calculate the intervals μ ± σ, μ ± 2σ, and μ ± 3σ. Find the probability that an observation will fall into each of these intervals.

f. Are the results of part e consistent with Tchebysheff€™s Theorem? With the Empirical Rule? Why or why not?

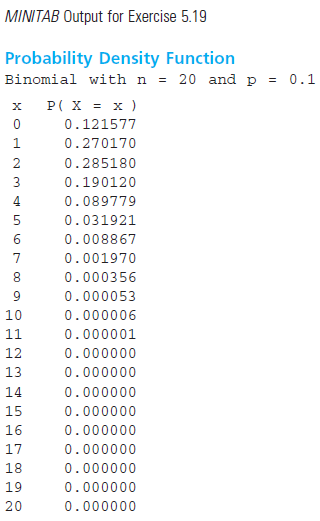
MINITAB Output for Exercise 5.19 Probability Density Function Binomial with n = 20 and p = 0.1 P( X = x ) 0.121577 0.270

MINITAB Output for Exercise 5.19 Probability Density Function Binomial with n = 20 and p = 0.1 P( X = x ) 0.121577 0.270170 0.285180 0.190120 0.089779 0.031921 0.008867 0.001970 0.000356 0.000053 10 0.000006 0.000001 11 12 0.000000 13 0.000000 0.000000 14 15 0.000000 0.000000 16 17 0.000000 18 0.000000 19 0.000000 20 0.000000

Step by Step Solution

★★★★★

3.42 Rating (171 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a so that Px 4 p0 p1 p2 p3 p4 9568255 b Using Table 1 Appendix ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction to business statistics Questions!

Q:

Let X be a binomial random variable with Pr(X = x) = (n/r)pXqn-x, x - 0, 1 2, . . ., n, where n (> 2) is the number of Bernoulli trials, p is the probability of success for each trial, ad q = 1 - p....

Q:

Let X be a binomial random variable with parameters n and p. Show that p)n+ n + Dp

Q:

Let X be a binomial random variable with parameters (n, p). What value of p maximizes P{X = k}, k = 0, 1, . . . , n? This is an example of a statistical method used to estimate p when a binomial (n,...

Q:

Let x be a binomial random variable with n = 20 and p = .1. a. Calculate P(x 2) using Table 1 in Appendix I to obtain the exact binomial probability. b. Use the Poisson approximation to calculate...

Q:

Let x be a binomial random variable with n = 20 and p = .1. a. Calculate P(x 4) using the binomial formula. b. Calculate P(x 4) using Table 1 in Appendix I. c. Use the Excel output below to...

Q:

5.19 Let X be a binomial random variable with n = 20 and p=0.1. a. Calculate P(X4) using the binomial formula. b. Calculate P(X 4) using Table 1 in Appendix I. c. Use the Excel output below to...

Q:

Questions are in the attachment. QUESTION 1 If X is a binomial random variable with n = 20 and p = 0.25, the mean of X is: Q a. 10 O b. 4 O c. 5 d. None of the above QUESTION 2 variable. A cumulative...

Q:

Suppose x is a binomial random variable with n = 4 and p = .4. a. Calculate the value of p1x2, x = 0, 1, 2, 3, 4, using the formula for a binomial probability distribution. b. Using your answers to...

Q:

Suppose x is a binomial random variable with n = 3 and p = .3. a. Calculate the value of p(x), x = 0, 1, 2, 3, using the formula for a binomial probability distribution. b. Using your answers to part...

Q:

1.Given a binomial random variable with n = 20 and p = 0.60, find the following probabilities using the binomial table. a. P ( X ? 13) b. P ( X ? 15) c. P ( X = 17) d. P (11 ? ...

Q:

Assume that the quantity of ending inventory is larger than the quantity of beginning inventory and that the lifo method is being used. Would operating income using direct costing be different from...

Q:

Write a paper in which you have to compare and contrast the business models; explain how strategic plans fit into these models, and how they can grow an organization.

Q:

The higher the percentage of a firm's total costs that are fixed, the higher the degree of operating leverage and the lower the operating breakeven point.

Q:

An increase in the market demand curve will shift the market supply curve as well. Defend or refute.

Q:

A businessman in New York is preparing an itinerary for a visit to six major cities. The distance traveled, and hence the cost of the trip, will depend on the order in which he plans his route. How...

Q:

Three students are playing a card game. They decide to choose the first person to play by each selecting a card from the 52-card deck and looking for the highest card in value and suit. They rank the...

Q:

A sample space contains 10 simple events: E1, E2,... , E10. If P(E1) = 3P(E2) = .45 and the remaining simple events are equiprobable, find the probabilities of these remaining simple events.

Q:

Cumulative preferred stock: A) has a right to vote cumulatively B) requires dividends in arrears to be carried over into the next period. C) has a claim to dividends after common stock D) generally...

Q:

Happy Cleaners needs a new steam finishing machine that costs $100,000. The company is evaluating whether it should lease or purchase the machine. The equipment falls into the MACRS 3-year class, and...

Q:

\# Your company is considering 2 projects, Project IOT and Project ERP, each of which requires and initial outlay of 50 million BDT. Your company uses a financial model for project selection, BCR and...