19. Let X denote a hypergeometric random variable with parameters n, m, and k.

That is,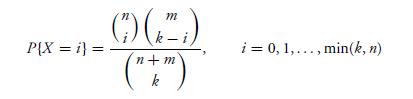 

(a) Derive a formula for P{X = i} in terms of P{X = i − 1}.

(b) Use part

(a) to compute P{X = i} for i = 0, 1, 2, 3, 4, 5 when n = m = 10, k = 5, by starting with P{X = 0}.

(c) Based on the recursion in part (a), write a program to compute the hypergeometric distribution function.

(d) Use your program from part

(c) to compute P{X ≤ 10} when n = m = 30, k = 15.

m ()() P{X = i} = n+m i = 0, 1,..., min(k, n)