A continuous random variable is said to have a Laplace(, b) distribution 14 if its PDF is given by fx(x) 26 2b 1 26 exp exp( ) exp( ) x b if x if...

a To find the expected value EX and variance VarX of a Laplace0 1 distributed random variable you ca ...

A continuous random variable is said to have a Laplace(, b) distribution [ 14 ] if its

Question:

A continuous random variable is said to have a Laplace(μ, b) distribution [14] if its PDF is given by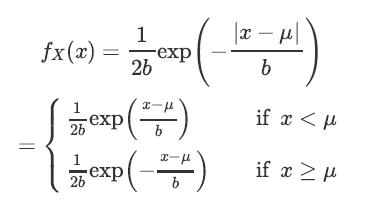 fx(x) = 26 2b 1 26 -exp exp(

where μ ∈ R and b > 0.

a. If X ∼ Laplace(0, 1), find EX and Var(X).

b. If X ∼ Laplace(0, 1) and Y = bX + μ, show that Y ∼ Laplace(μ, b).

c. Let Y ∼ Laplace(μ, b), where μ ∈ R and b > 0. Find EY and V ar(Y).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction To Probability Statistics And Random Processes

ISBN: 9780990637202

1st Edition

Authors: Hossein Pishro-Nik

See More Books

Question Posted: Oct 27, 2023 03:50 AM

See More Questions

A dagram of hypothetical 40 cm long arm is shown in figure 4.11. for the purposes of answering this question assume that the arm itself is weighless. if the muscle attached to the arm can contract at...
15. The Investment Club at Bell Labs has solicited and obtained $50,000 from its members. Collectively, the members have selected the three stocks, two bond funds, and a tax-deferred annuity shown in...
A continuous random variable is said to have a Rayleigh distribution with parameter if its PDF is given by where > 0. a. If X Rayleigh(), find EX. b. If X Rayleigh(), find the CDF of X,F X (x)....
Julie Hernandez is single and has no dependents. She operates a dairy farm and her Social Security number is 000-00-1111. She lives at 1325 Vermont Street in Costa, Florida. Consider the following...
Which two categories of costs influence the choice of how many storage facilities a firm might have and where they are located?
You are running for reelection as president of the nation of Utopia. Your opponents have criticized you for allowing the national debt to grow by almost 50 percent over the last 4 years. Use the...
Consider a process with the following streams: (a) Compute $\Delta T_{\text {thres }}$ as well as the minimum external heating and cooling requirements as a function of $\Delta T_{\text {min }}$....
Santos Company currently manufactures one of its crucial parts at a cost of $3.40 per unit. This cost is based on a normal production rate of 50,000 units per year. Variable costs are $1.50 per unit,...
22 Ibm of air under atmospheric pressure occupies a volume of 293 ft. What is the temperature of the air at that condition
Let X Laplace(0, b), i.e., where b > 0. Define Y = |X|. Show that Y Exponential (1/b). fx() 1 ) (E), exp 26 b
A company makes a certain device. We are interested in the lifetime of the device. It is estimated that around 2% of the devices are defective from the start so they have a lifetime of 0 years. If a...
The following pseudo-syntheses (guaranteed not to work) exemplify a common conceptual error. (a) What is the conceptual error implicit in these syntheses? (b) Propose syntheses that are more likely...
If Mr. Keating quits his job as a teacher to homeschool his own children, GDP a. stays the same because he is engaged in the same activity. b. rises because he now pays lower income taxes. c. falls...
If all quantities produced rise by 5 percent and all prices fall by 5 percent, which of the following best describes what occurs? a. Real GDP rises by 5 percent, while nominal GDP falls by 5 percent....
The largest component in the basket of goods and services used to compute the CPI is a. food and beverages. b. housing. c. medical care. d. apparel.
The goal of fundamental analysis is to a. determine the true value of a company. b. put together a diversified portfolio. c. predict changes in investor irrationality. d. eliminate investor risk...
The CPI measures approximately the same economic phenomenon as a. nominal GDP. b. real GDP. c. the GDP deflator. d. the unemployment rate.
Where are estimated income taxes reported on the statement of financial condition for personal financial statements?
Why is disclosure of depreciation or amortization methods and rates so important?
What management , organization, and technology factors should be addressed when deciding whether to allow employees to use their personal smartphones for work?
Compare the BYOD experiences of Michelin North America and Rosendin Electric. Why did BYOD at Michelin work so well?
Allowing employees to use their own smartphones for work will save the company money. Do you agree? Why or why not?
A whispering chamber is an elliptically arched chamber. A unique feature of a whispering chamber is that when a person standing at one focus of the ellipse whispers, he can be heard by a person...
Listed below are four potential errors or problems that could occur in the processing of cash transactions. Review each error or problem and using the drop - down answer box located beneath each one,...
why are not all indigenous people peasants but a lot of peasants are indigenous people

A continuous random variable is said to have a Laplace(, b) distribution [ 14 ] if its

Question:

fx(x) = 26 2b 1 26 -exp exp(") exp(-) |x-μ|| b if x < μ if χ Σμ

Step by Step Answer:

a To find the expected value EX and variance VarX of a Laplace0 1 distributed random variable you ca...View the full answer

Introduction To Probability Statistics And Random Processes

Students also viewed these Business questions