(A generalization of the law of total probability) Let B1, B2,, Bn be disjoint events on a sample space such that P(Bi) > 0,

(A generalization of the law of total probability) Let B1, B2,…, Bn be disjoint events on a sample space Ω such that P(Bi) > 0, for all i = 1, 2,…, n. Prove that for any event A on this sample space, the following holds: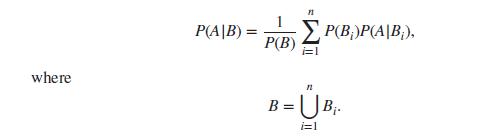

Explain how Proposition 3.5 can be deduced as a special case of this result.

where P(B)P(A|B), P(A|B) P(B) El B = = n B i=1