An approximation to Tukey HSD confidence intervals for mildly unequal sample sizes When the there are only small differences in the sample sizes, an approximation is available. The MSE and its degrees of freedom still come from the ANOVA table but \(\sqrt{2 M S E / n}\) is replaced by

\[\sqrt{M S E\left(\frac{1}{n_{i}}+\frac{1}{n_{\ell}}\right)}\]

Referring to the example concerning the drying time of glue on page 389 , use \(q_{0.05}=3.773\) with this approximate Tukey HSD approach to examine the three differences in means.

Data From Page 389

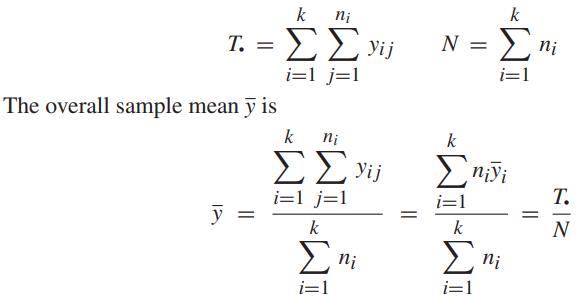
Observations Means Sum of Squares Sample 1: ... y11 y12 y1jY1n 1 (y1j-1) n2 Sample 2: ... y21 y22, y2j,. ,y2n2 .... y2 (y2j - y2) Sample i: Yil Yi2, Yij,..., Yini Yi IM nk (yij - Vi) (ykj-yk) Sample k: 1, 2,..., kj,..., nk j=1