Question: An engineer is measuring a quantity . It is assumed that there is a random error in each measurement, so the engineer will take n
An engineer is measuring a quantity θ. It is assumed that there is a random error in each measurement, so the engineer will take n measurements and report the average of the measurements as the estimated value of θ. Here, n is assumed to be large enough so that the central limit theorem applies. If Xi is the value that is obtained in the ith measurement, we assume that Xi = θ +Wi, where Wi is the error in the ith measurement. We assume that the Wi's are i. i. d. with EWi = 0 and Var(Wi) = 4 units. The engineer reports the average of the measurements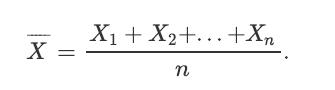
How many measurements does the engineer need to make until he is 90% sure that the final error is less than 0.25 units? In other words, what should the value of n be such that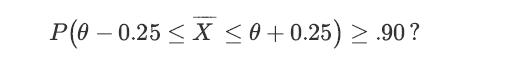
X X + X+...+Xn n
Step by Step Solution
3.27 Rating (165 Votes )
There are 3 Steps involved in it
Note that here the Xs are iid with mean and variance EX ... View full answer

Get step-by-step solutions from verified subject matter experts


