An industrial engineer collected data on the labor time required to produce an order of automobile mufflers using a heavy stamping machine. The data on times (hours) for \(n=52\) orders of different parts

\(\begin{array}{lllllllllll}2.15 & 2.27 & 0.99 & 0.63 & 2.45 & 1.30 & 2.63 & 2.20 & 0.99 & 1.00 & 1.05\end{array}\)

\(\begin{array}{lllllllllll}3.44 & 0.49 & 0.93 & 2.52 & 1.05 & 1.39 & 1.22 & 3.17 & 0.85 & 1.18 & 2.27\end{array}\)

\(\begin{array}{lllllllllll}1.52 & 0.48 & 1.33 & 4.20 & 1.37 & 2.70 & 0.63 & 1.13 & 3.81 & 0.20 & 1.08\end{array}\)

\(\begin{array}{lllllllllll}2.92 & 2.87 & 2.62 & 1.03 & 2.76 & 0.97 & 0.78 & 4.68 & 5.20 & 1.90 & 0.55\end{array}\)

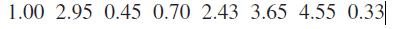
has \(\bar{x}=1.865\) hours and \(s^{2}=1.5623\) so \(s=1.250\) hours. What can one assert with \(95 \%\) confidence about the maximum error if \(\bar{x}=1.865\) hours is used as a point estimate of the true population mean labor time required to run the heavy stamping machine?

1.00 2.95 0.45 0.70 2.43 3.65 4.55 0.33