Assume our data Y given X is distributed Y | X = x ∼ Binomial(n, p = x) and we chose the prior to be X ∼ Beta(α,β). Then the PMF for our data is

and the PDF of the prior is given by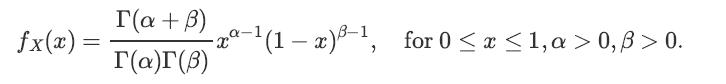

Note that,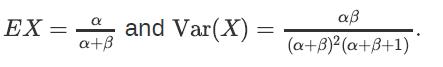

a. Show that the posterior distribution is Beta(α +y,β +n −y).

b. Write out the PDF for the posterior distribution, f_X|Y (x|y).

c. Find mean and variance of the posterior distribution, E[X|Y ] and Var(X|Y ).

Pr\x(ya) = (") x(1 x x(1-x)-y, for x = [0, 1], y = {0, 1,...,n},